A component that we may wish to study is usually a 3-dimensional object, but to view the component with the necessary resolution the shape is often lost. Therefore, it is crucial to 'think 3-D' when imaging sections. The images seen are profiles.

Truth may be obtained when the whole object is measured. Reallistically, we can only obtain an estimate of the truth. A characteristic of an estimate is a precision or degree of refinement of the measurement. The larger the sampling, the more precise an estimate can be.

Another estimate of truth is accuracy.

All stereological measurements are in principle obtained as relative measurements. In other words, as a ratio of at least two joint measurements, one relates to the components and the other relating to the structure as a whole. This is termed reference system.

Volume Density

Volume Density is defined as the volume of a component per unit volume of the containing reference space.

A. The principle of Delesse

The principle of Delesse is based on a cube containing only one component of irregular objects embedded in a matrix. The cube is sliced parallel to the x, z, plane in thickness of t. Each section has a total area of at on each section face the particle has an area of ap.

The volume of the particle in a section is:
vp = ap x t

The volume of the total section is:
vt = at x t

Take all the sections obtained from the cube and sum the volume of the particle over all the sections. Divide by the sum of the total volumes of all sections:

Replace vp with ap x t and vt with at x t then,

It figures that:

• The estimate of AA on unbiased sections will be an unbiased estimate of VV.
• The estimate of VV is independent of the shape of the reference space and the component's shape and distribution.

B. Examples

• Volume of mitochondria per volume of liver cell
• Volume of slow-twitch muscle cells per volume of skeletal muscle
• Volume of chloroplasts per volume of a leaf
• Volume of gold per volume of rock in a gold mine

C. Ways to measure area

1. Paper weighing

2. Planimetry
3. 
Linear analysis
4. 
Square counting

5. Point counting

6. Electronic planimetry (digitizing)

7. Automatic image segmentation

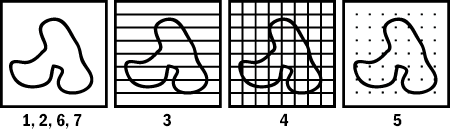
For many purposes, point counting is an efficient method.

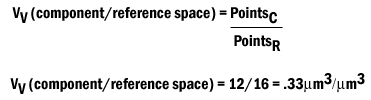
Surface Density

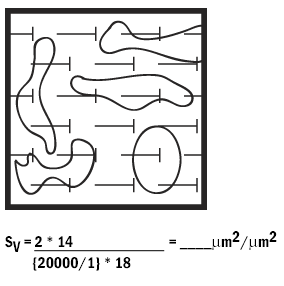
Surface density (Sv) is defined as the surface area of a component per volume of the reference space.

A. Example

Surface density of golgi within liver cells

Length Density

Length density (Lv) is the length of a component per volume of reference space.

A. Examples

• The length density of the capillaries within the glomerulus
• The length density of the proximal tubules within the kidney

The intersection of a tubular structure contained within a reference volume forms a profile on an intersecting plane. The longer the tubular structure, the more times it will intersect the section, forming more profiles. If Qc is the number of profiles seen on a section plane and AR is the reference area within the section, then

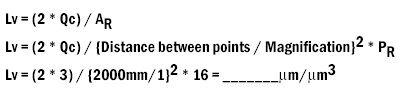
Numerical Density

Numerical density is the number of particles per unit volume of reference space.

A. Examples

• The number of mitochondria per unit volume of liver cell
• The number of glomeruli per unit volume of kidney
• The number of nuclei per unit volume of tumor

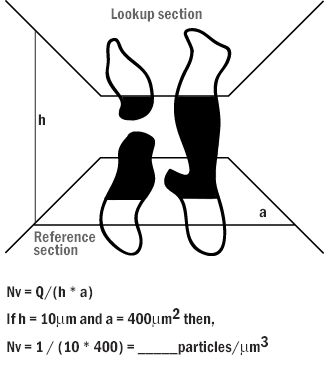
Numerical denisty is the most difficult of the 4 parameters to measure from tissue sections. Therefore, one needs a 3-D probe to quantify particle number. A 3-D probe is the dissector (2 parallel sections a known distance apart).

The dissector principle is a technique that allows for unbiased estimation of Nv independent of particle size and shape. To use this technique, 2 parallel sections from the reference space are needed that are separated by a known distance h. On 1 section, the reference section, a set of profiles are selected using the unbiased counting frame known area a. All the profiles selected are then looked for in the lookup section. Q is the number of profiles selected on the reference section that is not present in the lookup section.

Profiles of the same particle must be identifiable as being from the same particle in the 2 sections if present in the 2 sections. A profile cannot be hidden behind another profile and thus not be identifiable.

Vv, Sv, Lv and Nv are ratios between the component and the reference volume. You do not know the volume, surface, length or number of anything, only the ratio. If you measure the volume of the reference space, you may then calculate the volume, area, length or number of the component.

Volume

Volume displacement is the amount of liquid diplaced when a sample is immersed in liquid.

Cavalieri principle- for a fairly regular particle there should be 7-10 sections through the particle to obtain a precise estimate of the volume.